Standard Deviation in Mutual Fund: What is Standard Deviation in Mutual Fund

Standard Deviation in Mutual Fund: Meaning, Importance & Calculation

Updated on 27 Nov, 2024

Reviewed by

Fact checked by

5 Mins

What is Standard Deviation in Mutual Fund?

A standard deviation is a statistical tool that helps measure the deviation in portfolio returns from its average. The standard deviation has wide use in determining the risk of an investment. It is an important metric to consider while investing in market-linked instruments. Since markets are volatile, the returns fluctuate on a daily basis. These fluctuations depend on various internal and external factors.

Indicative returns of 10-12% annually

Investment horizon of 5+ Years

No lock-in

Long term goals such as retirement or building your wealth

Parag Parikh Flexi Cap fund (G)

HDFC Large and Mid Cap Fund (G)

ICICI Prudential Value Discovery Fund (G)

ICICI Prudential Bluechip Fund (G)

The Standard deviation of a mutual fund reflects its volatility. For a mutual fund, it shows how far the returns deviate from the expected returns based on its past performance.

A higher standard deviation implies a higher variation in returns, and a lower value indicates a lower range. It is the deviation in returns from the average over time.

You cannot decide if the standard deviation of a fund is high or low unless you compare it to other schemes in the same category. Low-risk schemes such as debt mutual funds tend to have a low standard deviation. While funds in the equity category will have a higher standard deviation in comparison to the debt category.

In practice, the standard deviation is estimated using 3, 5 and 10 year trailing monthly returns. Furthermore, all the monthly standard deviation values are annualised and represented as a percentage.

Importance of Standard Deviation in Mutual Funds

Following is the importance of standard deviation in mutual funds:

Measures Total Risk: Standard deviation considers the total risk rather than just the market-related volatility. Therefore, it is a broader metric than beta.
Useful for Both Equity and Debt Schemes: Standard deviation helps gauge the variability in returns for both equity and debt schemes.
Matching Risk Level: Using standard deviation, you can match the risk level of a mutual fund to your own risk tolerance levels.
Indicator of Future Performance: Standard deviation is an indicator of the future performance of a mutual fund. In other words, using the standard deviation value, you can estimate the returns of a fund (going up or down) from its mean/ average returns.
Comparing Similar Funds: You can compare funds belonging to the same category. A considerably different standard deviation from similar funds could indicate that your fund’s operations differ in some way (good or bad).

How to Calculate Standard Deviation of mutual fund?

The standard deviation of a mutual fund shows the riskiness of the fund. The higher the standard deviation, the higher the fund’s volatility. And, higher the volatility of the fund, the higher is its risk. Using the below formula, you can compute the standard deviation for a mutual fund:

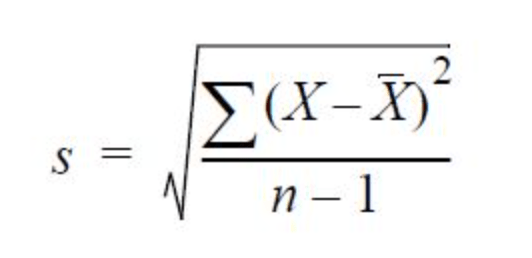
Following is a step-by-step procedure to compute standard deviation:

List down the yearly mutual fund returns (Investment returns – X)
Compute the mean of the investment returns (Average Return – X̅)
Subtract each year’s return from the mean (X – X̅)
Square each year’s deviation (X – X̅)²
Add all the values
Divide the sum by the total number of periods – 1 (n-1)
Take a square root of the obtained value to determine the standard deviation.

Let’s understand the calculation with a simple example.

Year	Yearly Mutual Fund Return (X)	Deviation from Mean (X – X̅)	(X – X̅)²
1	15	4.60	21.16
2	12	1.60	2.56
3	20	9.60	92.16
4	-5	-15.40	237.16
5	10	-0.40	0.16

Mean (X̅) = 10.4

Σ(X – X̅)² = 353.20

n-1 = 4

Variance = 88.3

Standard Deviation = 9.40 (Square Root of Variance)

The standard deviation of 9.40 indicates that the fund’s returns would go up or down by this value from its mean.

Interpretation of Standard Deviation

Standard deviation measures the riskiness of a mutual fund. Equity schemes have a higher standard deviation in comparison to debt schemes.

Standard Deviation Value: Mutual fund returns would go up or down by the value of the standard deviation of that fund from its mean.
Gauge Returns: Historical data collected concerning the standard deviation will help you gauge the returns from a mutual fund in the future.
Positive and Negative Deviation: Standard deviation considers both the positive and negative deviation from the average. This means that above-average returns will increase the standard deviation in the same manner that below-average returns do. The positive deviation is always preferred when compared to negative deviations.
Duration: For long durations, the standard deviation tends to be lower. While for shorter periods, the value is usually higher.
Compare Funds Belonging to the Same Category: Standard deviation makes sense when comparing funds belonging to the same category and asset class. The comparison is more meaningful if the time frame is also the same. Furthermore, if a fund has a high standard deviation and belongs to a sector or category with a high standard deviation, it doesn’t mean the fund is highly volatile. In comparison to its category, the fund reflects similar volatility. Hence it is important to compare funds belonging to the same category.
High or Low Standard Deviation: High standard deviation doesn’t imply that a fund is good or bad. There can be funds that have generated significant returns and have a high standard deviation. On the contrary, funds with high negative returns from the average returns can have a high standard deviation. Hence, don’t consider standard deviation in isolation. Use it in conjunction with other metrics such as Sharpe ratio, Alpha, Beta, etc.