Compound Interest Calculator Online India – Power of Compounding
Estimate how much money you can make by using the power of compounding. The compound interest calculator will estimate the maturity amount when interest gets compounded monthly, quarterly, annually.
What is Compound Interest?
Compound interest in simple terms means interest on interest. When the principal includes the accumulated interest of the previous periods and interest is calculated on this then they say it’s compound interest. Compounding is done on loans, deposits and investments. Frequency of compounding is basically the number of times the interest is calculated in a year. Daily, weekly, monthly, quarterly, half-yearly and annually are the most common compounding frequencies. The higher the frequency of compounding, the greater the amount of compound interest. Also, the frequency of compounding depends on the instrument. A credit card loan is usually compounded monthly and a savings bank account is compounded daily.
Albert Einstein rightly said, “Compound interest is the 8th wonder of the world. He who understands it earns it and he who doesn’t pays it.” Compounding is a very powerful concept. This is because the interest of your invested money is also earning interest. The value of the investment keeps growing at a geometric rate (always increasing) than at an arithmetic rate (straight-line). Your money keeps on multiplying over a period of time. Also, if paying interest is ignored, or if there is any delay in paying the loan, then the interest burden will surely be high. Also, to take advantage of compounding, one has to increase the frequency of loan payments. This way, they can pay lesser interest than what they are liable to pay.
Investing in mutual funds is one of the easiest way of reaping the benefits of compounding. Opting to reinvest dividends or choosing a growth plan results in purchasing more shares of the fund. More interest accumulates over time through continuous purchasing, and also the investment will grow in value.
What is the Power of Compounding?
Reinvestment of earnings at the same rate of return to grow the principal amount every year is compounding. Compounding is a compelling concept. It is because the interest of your invested money is also earning interest. This is known as compound interest. The value of the investment keeps growing at a geometric rate (always increasing) rather than at an arithmetic rate (straight-line). Reinvestment of earnings at the same compound interest rate of return would help in continually growing the principal amount year-on-year.
When the principal includes the accumulated interest of the previous periods and interest is calculated on this then they say its compound interest. This powerful tool (compound interest) can be used by investors to plan their financial goals. In the long term, this technique will benefit the investor. Longer, the investment horizon higher are the returns. The right advice is to start saving regularly and invest wisely. An early start would give the investor a higher compounding effect, and building wealth becomes easy. The possibilities of the compound interest are endless. With time, compound interest only further enhances the earnings, and the investment grows manifold.
Compound interest can be calculated by:
- Daily compounding
- Monthly compounding
- Quarterly compounding
- Half-yearly compounding
- Yearly compounding
Compounding is done on loans, deposits and investments. Frequency of compounding is basically the number of times the interest is calculated in a year. The higher the frequency of compounding, the greater the amount of compound interest. The frequency of compounding depends on the instrument. A credit card loan is usually compounded monthly and a savings bank account is compounded daily. The frequency of compounding varies based on the scheme offered by the bank or financial institutions.
One doesn’t have to be a financial analyst to understand the concept of compounding. To make the maximum advantage of the compound interest, invest a small amount regularly for long periods of time. Use the compound interest calculator to see how the magic unfolds with time. Compounding is a technique that makes money work harder. An average investor depends on this tool to plan for their financial goals. Most long term financial goals become easier and achievable because of the power of compounding .
For example, INR 100 is invested, and the compound interest rate is 6% p.a. The principal amount is INR 100, and the interest earned at the end of 1 year is INR 6 (6% of INR 100). Instead of withdrawing the interest amount, it is reinvested, then the principal amount for the second year becomes INR 106 (INR 100 + INR 6). The interest earned for the second year is INR 6.36, this is 0.36 more than the previous year. Even though the amounts look very small, it makes a huge difference in the long term. The magic of compounding works only over long periods of time.
How to Use the Compound Interest Calculator?
Use Scripbox’s Compound Interest calculator to find how much corpus you would earn at the end of your investment period.
Here, all you need to do is enter the principal amount you want to invest and the time period. Let’s understand how to use the power of compounding calculator step-by-step with an example.
- Firstly, choose the type of investment – monthly or one time and enter the investment amount. Let’s say, Ms Darsha make a one-time investment of INR 1,50,000.
- Next, choose the compounding interval – monthly, semi-annually, quarterly, or annually. Here, Darsha’s compounding interval is annual.
- Lastly, select the investment tenure and interest rate. Use the slider to choose the appropriate rate. Darsha’s investment horizon is 10 years and the interest rate is 8%.
For the above inputs, Scripbox’s compound interest calculator automatically calculated the maturity amount. For Ms Darsha, her maturity amount at the end of 10 years will be INR 3,23,839. Interest earned is INR 3,23,839 – INR 1,50,000 = INR 1,73,839.
Furthermore, you can change the inputs and try various combinations to estimate the potential returns from your investment.
Scripbox offers a monthly compound interest calculator, quarterly compound interest calculator, semi-annual compound interest calculator, and annual compounding calculator.
Advantages of Compound Interest Calculator in India
The following are the advantages of using Scripbox’s online Compound Interest Calculator:
- Easy to use: The compound interest calculator is straightforward to use. All the investor has to do is enter the amount of investment, investment tenure and interest rate.
- Time-saving: Using the online compound interest rate calculator can save an investor’s time. Investors don’t have to go through the hassle of manually performing complex calculations. The calculator will generate results within seconds.
- Accuracy: The compound Interest calculator is built with precision. Thus, the calculations are always accurate.
- Future planning: Investors can plan their financial future in a better way. The compound interest maturity value calculator returns the amount their investment will reap upon maturity.
- Free to use: Investors can use the compound interest calculator multiple times for free of cost.
How to Calculate Compound Interest?
The compound interest formula is as follows:
Compound Interest = Total amount of Principal and Interest in future (or Future Value) less Principal amount at present (or Present Value)
Compound Interest = P [(1 + i) n – 1]
P is principal, I is interest rate, n is number of compounding periods.
An investment of Rs 1,00,000 for 5 years at 12% rate of return compounded annually is worth Rs 1,76,234. From the graph below we can clearly see how an investment of Rs 1,00,000 has grown in 5 years.
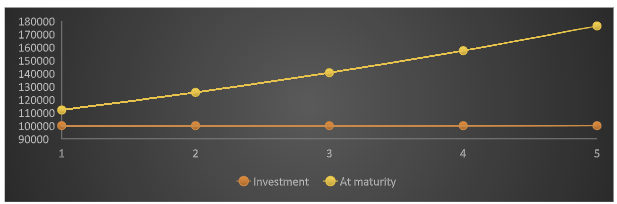
In compound interest one earns interest on interest. Therefore, the investment already includes all the previous interests. And interest is paid on that.
| Year | Investment(Rs) | Interest(Rs) | At Maturity(Rs) |
| 1 | 1,00,000 | 12,000 | 112,000 |
| 2 | 1,12,000 | 13,440 | 125,440 |
| 3 | 1,25,440 | 15,052.8 | 1,40,492.8 |
| 4 | 1,40,492.8 | 16,859.14 | 1,57,351.9 |
| 5 | 1,57,351.9 | 18,882.23 | 1,76,234.2 |
By understanding the importance of compound interest and acting on it by investing in appropriate investments, one can achieve high returns.
Compounding Intervals
The frequency of compounding and wealth accumulation are directly related. The higher the frequency of compounding, more the accumulation of wealth. Let’s look at the example of Rs 10,000 at 10% interest compounded for different frequencies.
| Time | Annual | Quarterly | Monthly |
| 1 | 11,000.00 | 11,038.13 | 11,047.13 |
| 5 | 16,105.10 | 16,386.16 | 16,453.09 |
| 10 | 25,937.42 | 26,850.64 | 27,070.41 |
It is very clear from the above example that the higher the compounding interval, higher is the wealth accumulated. Also, longer the investment tenure higher is the wealth accumulated.
Let the magic of compounding work for you by investing regularly and staying invested for long horizons and increasing the frequency of loan payments. By familiarizing yourself with such concepts you can make better financial decisions and earn higher returns.
How Does Compound Interest Work?
Compound interest earns interest not only on your initial investment but also on the interest accumulating over time. It allows your money to grow exponentially, as the interest is calculated on both the principal amount and any previously earned interest. Thus, you are earning interest on your interest as well. Compound interest is a powerful financial concept that can lead to significant investment growth over time.
Three factors affect your compound interest returns:
- Time: The longer you invest, the more your money grows.
- Interest Rate: A higher interest rate means a higher balance with compound interest.
- Compounding Interval: The more frequently interest is compounded, the faster your money will grow.
Simple Interest Vs Compound Interest
Having simple interest for loans is very easy as the interest payments are standard. But when it comes to investments, one can earn more from compound interest. The basic difference between simple and compound interest is that the interest is not added to the principal in simple interest. To earn interest on interest one has to immediately reinvest the interest earned. But in compounding this happens automatically with no extra effort needed.
Simple interest is calculated with a simple formula which is Principal*interest rate*tenure. The simple interest amount remains same through the tenure of the investment or loan. It is easy to calculate than compound interest.
The return from compounding is higher than that of simple interest.
The interest earned grows rapidly in compound interest and in simple interest it remains constant.
The principal amount in simple interest remains constant, while in compound interest the principal amount keeps increasing as the interest from previous periods add to it.
Also, having a loan in simple interest ensures standard interest payments. But in compounding the interest payment comes down as the principal is being repaid. If not repaid on time the interest burden keeps increasing.
Let’s look at an example of an investment of Rs 1,00,000 invested for 5 years earning an interest of 12% both in simple and compound interest.
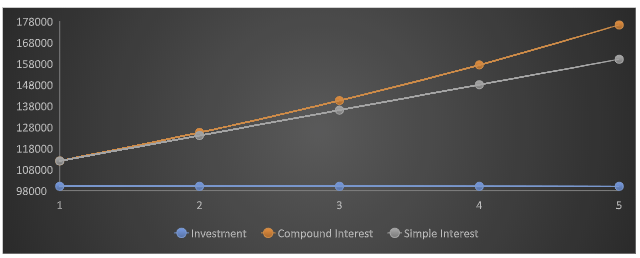
Its clear that at maturity the amount from compounding is higher than that from simple interest. The investment value increases at faster pace in compounding. With the same initial investment at the same interest rate for a same tenure the gain from compounding is higher than from simple interest. Even with a complex calculation, compounding is beneficial than simple interest. Compounding is more of a real time concept than simple interest.
Understand the Difference between simple vs compound interest rate
Frequently Asked Questions
The effective annual rate is the rate that actually gets paid after all of the compounding. When compounding of interest takes place, the effective annual rate becomes higher than the overall interest rate. Thus, the more times the interest is compounded within the year, the higher the effective annual rate will be.
Yes, the online interest calculators generally ask you to enter the amount, rate of interest, time period, etc, manually so that you can get dynamic results as per needs.
In compound interest, the investment grows much faster than the simple interest as the interest is paid on both investments and previous interest.
Let’s calculate the interest income for an investment of Rs 1 lakh at a rate of 20% p.a. for a period of 3 years.
The simple interest earned will be I= P*R*T/100
That is, I = 1,00,000*20*3/100 = Rs 60,000
And in case of compound interest, amount is P (1 + r/n) ^ not
That is, A=1,00,000(1+0.2) ^3 = 1,00,000(1.728) = 1,72,800
Hence, I = A-P i.e. 1,72,800-1,00,000 = Rs 72,800
You can see it yourself that there is a great difference in the returns between the two. Therefore, compound interest proves to be a good option for investment the return is higher than simple interest.
The compound interest calculator includes the following compounding options:
Daily compounding
Monthly compounding
Quarterly compounding
Half yearly compounding
Yearly compounding
With savings accounts, the interest compounding is at either the start or the end of the period (month or year).
For a monthly instalment of ₹12,000 compounded every month for 4 years at 5% interest rate, the maturity amount would be ₹6,36,179. The total interest earned is ₹60,179.